의사 결정 트리(Decision Tree)

의사 결정 트리는 분류(Classification) 기술 중 가장 일반적으로 사용되는 방법입니다. 의사 결정 트리의 개념이 익숙하진 않겠지만 대표적으로 예를 들을 수 있는 것이 바로 스무고개라는 게임입니다. 스무고개는 총 20개의 질문만 허락되며, 그에 대한 답변으로 ‘예’ 혹은 ‘아니오’로만 대답하여서 추측하여 답에 도달하는 게임이죠. 의사 결정 트리를 표현하는 방법은 다음 그림과 같습니다.

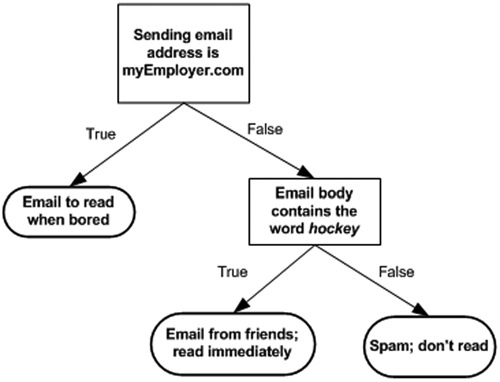
위의 그림에서 사각형을 decision block이라고 하고 타원형을 terminating block이라고 합니다. 그림에서의 질문에 대답으로 어떤 결론에 도달하게 되는데 결론에 도달하기 전에 뻗어나가는 화살표를 branches라고 합니다.

1. 트리구조

의사 결정 트리를 구성하기 위해서는 decision을 만들어야 하는데 decision은 데이터 분할에 영향을 주는 attribute로 결정됩니다. 의사 결정 트리를 만드는 순서는 아래와 같습니다.

위의 내용을 의사코드로 표현하면 아래와 같습니다.

createBranch function()
Check if every item in the dataset is in the same class:
    If so return the class label
    Else
        find the best feature to split the data
        split the dataset
        create a branch node
            for each split
                call createBranch and add the result to the branch node
        return branch node

2. 데이터 분할 방법 (의사 결정 트리 알고리즘)

대표적인 의사 결정 트리 알고리즘은 다음과 같습니다.

이번 포스팅에서는 가장 기초가 되는 ID3을 기준으로 설명할 예정입니다.

2.1 Information gain

데이터를 분할하기 전과 후의 변화를 Information gain이라고 합니다. 데이터 집합에 대한 정보 측정 방법을 Shannon entropy 또는 엔트로피라고 합니다. 엔트로피는 정보에 대한 기대 값이라고 할 수 있습니다. 다양한 값을 가질 수 있는 어떤 데이터를 분류하고자 한다면, 정보 $ x $로 표시하고 다음과 같이 정의할 수 있습니다. $$ l(x) = \log_2p(x) $$ 여기서 $ p(x) $는 $ x $라는 분류 항목이 선택될 확률입니다. 엔트로피를 계산하기 위해서는 분류 항목의 가능한 모든 값에 대해 모든 정보의 기대 값이 필요한데 엔트로피는 아래의 식에 의해서 계산됩니다. $$ H(S) = -\sum_{x \in X}p(x)\log_2p(x) $$ 위에서 Information gain은 데이터를 분할하기 전과 후의 변화라고 이야기 했는데, 즉 이 말은 어떤 속성을 선택함으로 인해서 데이터를 더 잘 구분하게 되는 것을 의미합니다. 예를 들어 학생 데이터에서 수능 등급을 분류하는데 있어 수학 점수가 체육 점수보다 변별력이 높다고 가정합시다. 그러면 수학 점수 속성이 체육 점수 속성보다 Information gain이 높다고 할 수 있겠습니다. 정보 이득의 계산 식은 아래와 같습니다. $$ IG(A,S) = H(S) -\sum_{t \in T}p(t)\log_2p(t) $$

여기서 앞의 $ H(S) $는 상위 노드의 엔트로피를 의미합니다. 그러면 Information gain의 계산 식은 상위 노드의 엔트로피에서 하위 노드의 엔트로피를 뺀 것이 됩니다. 뒤의 식은 하위 각 노드의 엔트로피를 계산한 후 노드의 속한 레코드 수를 가중치로 하여 엔트로피를 평균한 값입니다. 즉 $ IG(A) $는 속성(Feature) A를 선택했을 때 Information Gain을 계산하는 식으로, 원래 노드의 엔트로피를 구한 값을 $ I $라고 하면, 속성 $ A $를 선택한 후의 x개의 하위 노드로 나누어 진 것에 대한 전체 엔트로피를 구한 후 그것을 J라고 할 때 $ I-J $를 의미하는 것입니다. 이때 이 결과의 값이 클 수록 Information gain이 큰 것이고 속성 A가 분류하기 가장 좋다는 것을 의미합니다.

3. 정리

Decision Tree의 장단점

이 포스팅에서는 ID3를 사용한 Decision tree에 대해 알아보았습니다. ID3는 수치형 값을 다룰 수 없는 단점이 있기 때문에 연속형 값은 양자화(Quantization)를 통해 이산 방식으로 변형해야 합니다. 그러나 너무 많은 분할이 이루어질 경우 또 다른 문제가 발생할 수 있습니다.

Reference



comments powered by Disqus
#머신러닝 #의사결정트리 #machine learning #decision tree #id3 #cart #c4.5