딥러닝(Deep Learning) 살펴보기 1탄

이번 포스트에서는 Deep learning에 대해 살펴볼 예정입니다. 이번 포스트는 Reference에 있는 내용을 정리한 것입니다. Deep learning은 대세가 되었습니다. 주변에서 딥러닝이라는 이야기가 많이 들립니다. 딥러닝이란 무엇인지 알아보도록 하겠습니다. 오늘날 딥러닝을 가능하게 해준 3가지가 있습니다.

그럼 딥러닝을 이용해서 할 수 있는 것을 한번 볼까요? 딥러닝의 가장 좋은 활용 사례라고 할 수 있는 이미지 인식을 한번 보도록 할게요. 컴퓨터에게 동물의 그림을 보고 맞출 수 있도록 하는 것이 그 예가 되겠습니다. 그럼 코드로 바로 볼까요?

def VGG16(include_top=True, weights='imagenet',
        input_tensor=None, input_shape=None,
        pooling=None,
        classes=1000):
# 중략 ...

# Block 1
x = Conv2D(64, (3, 3), activation='relu', padding='same', name='block1_conv1')(img_input)
x = Conv2D(64, (3, 3), activation='relu', padding='same', name='block1_conv2')(x)
x = MaxPooling2D((2, 2), strides=(2, 2), name='block1_pool')(x)

# Block 2
x = Conv2D(128, (3, 3), activation='relu', padding='same', name='block2_conv1')(x)
x = Conv2D(128, (3, 3), activation='relu', padding='same', name='block2_conv2')(x)
x = MaxPooling2D((2, 2), strides=(2, 2), name='block2_pool')(x)

# Block 3
x = Conv2D(256, (3, 3), activation='relu', padding='same', name='block3_conv1')(x)
x = Conv2D(256, (3, 3), activation='relu', padding='same', name='block3_conv2')(x)
x = Conv2D(256, (3, 3), activation='relu', padding='same', name='block3_conv3')(x)
x = MaxPooling2D((2, 2), strides=(2, 2), name='block3_pool')(x)

# Block 4
x = Conv2D(512, (3, 3), activation='relu', padding='same', name='block4_conv1')(x)
x = Conv2D(512, (3, 3), activation='relu', padding='same', name='block4_conv2')(x)
x = Conv2D(512, (3, 3), activation='relu', padding='same', name='block4_conv3')(x)
x = MaxPooling2D((2, 2), strides=(2, 2), name='block4_pool')(x)

# Block 5
x = Conv2D(512, (3, 3), activation='relu', padding='same', name='block5_conv1')(x)
x = Conv2D(512, (3, 3), activation='relu', padding='same', name='block5_conv2')(x)
x = Conv2D(512, (3, 3), activation='relu', padding='same', name='block5_conv3')(x)
x = MaxPooling2D((2, 2), strides=(2, 2), name='block5_pool')(x)

# 중략...

# Create model.
model = Model(inputs, x, name='vgg16')

# load weights
if weights == 'imagenet':
    if include_top:
        weights_path = get_file('vgg16_weights_tf_dim_ordering_tf_kernels.h5',
                                WEIGHTS_PATH,
                                cache_subdir='models')
    else:
        weights_path = get_file('vgg16_weights_tf_dim_ordering_tf_kernels_notop.h5',
                                WEIGHTS_PATH_NO_TOP,
                                cache_subdir='models')
    model.load_weights(weights_path)

# 중략 ...
return model

코드를 보니 쉽지 않은 것 같아 보입니다. 참고로 저는 케라스로 코드를 짜보거나 케라스의 문서를 본적도 없습니다. 그러나 앞으로 정리한 내용을 보게 되면 위의 코드가 어떻게 돌아가는지 이해하게 될겁니다.

Neural Network 복습하기

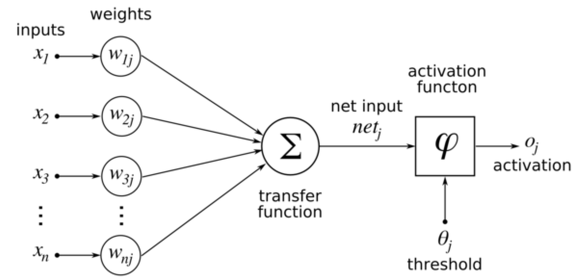
하나의 뉴런을 모델링한 것을 나타낸 그림입니다. 이러한 뉴런들이 모여서 아래와 같이 뉴럴 네트워크를 구성하게 됩니다.

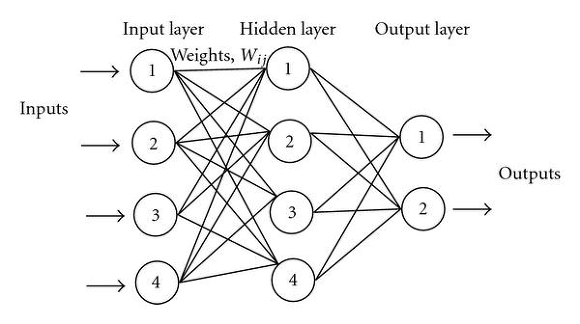
위의 그림에서 하나의 컴포넌트가 뉴런을 나타내고 있는 것이죠. 아마 이 그림을 보면 위의 그림들이 이해가 될 것입니다.

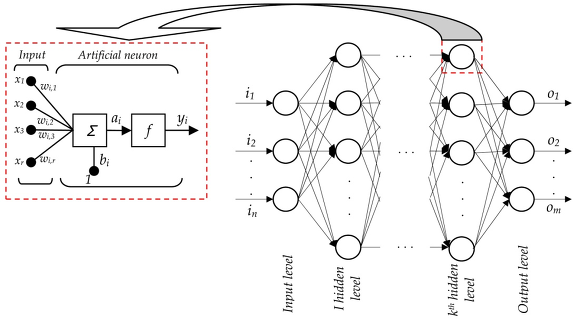
이러한 형태로 구성된 것이 바로 뉴럴 네트워크 입니다. 인간의 뇌를 모델링해서 컴퓨터에서도 비슷하게 동작하도록 만든 것입니다. 그럼 딥 러닝은 무엇일까요? 뉴럴 네트워크의 레이어를 깊게 쌓은 형태를 DNN(Deep Neural Network)라고 합니다.

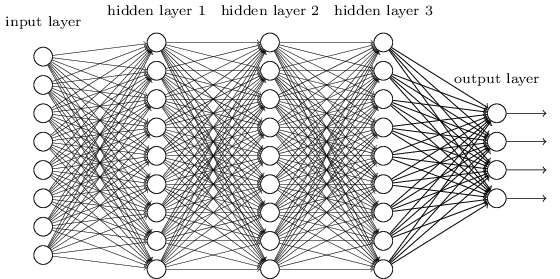
통상 이렇게 깊게 쌓은 형태의 뉴럴 네트워크를 딥러닝이라고 하고 있죠. 물론 딥러닝과 딥뉴럴넷이 같다는 것은 아닙니다. 사람의 뇌를 모델링한 것이니까 사람이 하는 것들을 할 수 있을 것이라고 생각했지만 실제론 잘 안됩니다. 다음과 같은 문제점들이 있기 때문이죠. 바로 이러한 문제점들을 해결하기 위한 노력이 딥 러닝을 연구하는데 핵심이 되는 것입니다. 어떠한 문제를 가지고 있는지 살펴보도록 하겠습니다.

딥러닝의 문제점

딥러닝의 문제점은 크게 3가지 관점에서 볼 수 있습니다. 주로 모델을 얼마나 잘 학습 시킬 것인지에 관한 문제입니다. 얼마나 잘 학습 됐는지가 바로 모델의 성능의 척도가 되기 때문입니다. 3가지의 문제점을 요약하면 다음과 같습니다.

그럼 각각의 문제점들에 대해서 좀 더 상세히 살펴보도록 하겠습니다.

Underfitting

Underfitting은 학습이 잘 안되는 문제를 이야기합니다. 그러면 왜 이러한 문제가 발생할까요? 문제가 발생하는 원인을 알아보려면 먼저 Neural Network의 학습 방식에 대해서 알아야 합니다. 뉴럴 넷의 학습 방법은 바로 Back propagation 알고리즘을 사용합니다. Back propagation을 번역서에서는 역전파라고 번역이 되어 있어서 어려워 보일 수가 있는데 그냥 간단하게 뒤로 전달한다는 의미입니다. 어렸을 때 운동장에 줄을 서있고 뒷사람에게 말을 전달하듯이 말이죠.

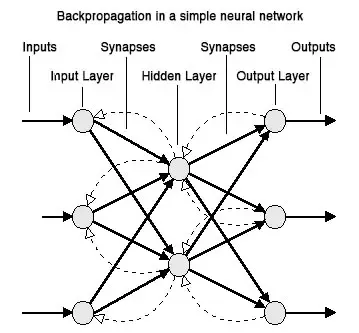
back propagation을 통해서 뒤로 전달하는 값은 바로 내가 틀린정도를 알려주는 것입니다. 내가 틀린 정도를 미분(기울기를 알아내서)하여 뒤로 전달하면서 올바른 방향으로 갈 수 있도록 weight 값을 조정하는 것이죠. 결국 미분하고, 곱하고, 더하고 뒤로 전달하면서 업데이트를 하는 것입니다. 그런데 여기서 한가지 문제가 있습니다. 전통적으로 뉴럴 넷의 경우 뉴런의 activation function을 sigmoid 함수를 사용하고 있었습니다. 여기서 activation function은 들어온 데이터를 다음으로 전달할 것이냐 말 것이냐를 결정하는 기준치라고 보시면 되겠습니다. sigmoid 함수는 아래와 같습니다.

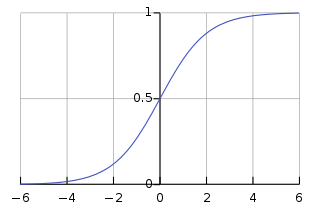
그럼 왜 sigmoid 함수가 문제가 될까요? 앞서 설명했듯이 학습을 하기 위해서 내가 틀린 정도를 미분하여 뒤로 전달한다고 했습니다. 여기서 미분이 바로 문제가 됩니다.

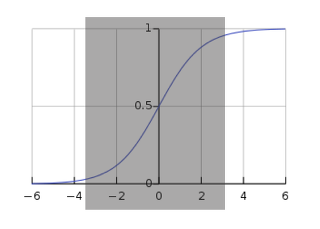
미분을 해서 뒤로 전달을 하게 되는데 위 그림에 있는 부분에서 미분이 되는 경우 그래도 값이 뭐라도 있으므로 뒤로 값이 전달됩니다.

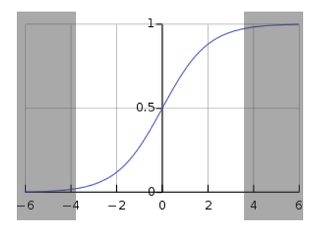
그러나 위의 그림처럼 해당 부분을 미분을 하면 0이나 0에 가까운데 이것을 중간에 곱해서 전달하게 되면 실제로 전달되는 값이 없게 됩니다. 그런데 이것을 학습시키기 위하여 계속 반복합니다. 그러면 input layer에 가까워질 수록 전달 받는 값이 없어서 업데이트가 없게 되는 것이죠. 이러한 현상을 바로 Vanishing Gradient라고 합니다. Vanishing Gradient 때문에 fitting이 잘 안되는 것을 바로 Underfitting이라고 하는 것입니다.

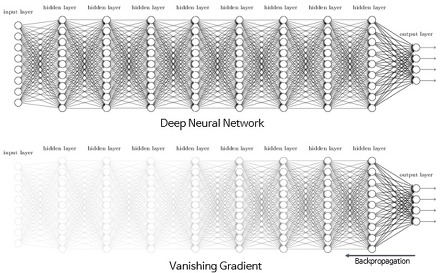
위의 그림에서 처럼 input layer에 가까운 layer들을 전달받는 값이 사라져서 학습이 잘 안되는 문제가 발생하게 되는 것이죠. 그러면 이러한 문제는 어떻게 해결할까요? 해결 방법은 바로 input layer까지 값이 잘 전달될 수 있는 activation function을 쓰는 것입니다. 그것이 바로 그 유명한 ReLU 입니다.

ReLU(Rectified Linear Unit)

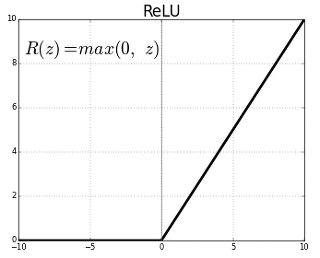
ReLU는 바로 위와 같은 형태입니다. 함수가 정말 간단합니다. 그럼 ReLU의 장점은 무엇일까요?

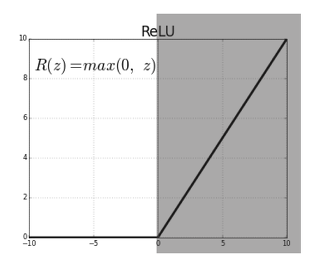
그건 바로 sigmoid과는 다르게 미분을 하여도 값이 사라지지 않게 해서 input layer까지 error 값을 전달할 수 있게 되는 것이죠. 왜냐하면 ReLU를 보면 양의 구간에서 미분값이 전부 1이기 때문입니다.

Underfitting 결론

Underfitting은 모델이 학습이 잘 되지 않는 것이 문제였습니다. 학습을 하는 과정에서 에러를 교정하기 위한 값이 앞쪽(input layer)까지 전달되어야 하는데, 이전에 많이 사용하던 activation function인 sigmoid의 경우에 값이 전달되다가 사라지는 Vanishing Gradient가 발생하여 학습이 되지 았습니다. 그래서 Vanishing Gradient를 해결하기 위해서 미분 값이 사라지지 않는 ReLU를 이용하여 학습이 더 잘 되도록 하였습니다.

이번 포스트에서는 딥러닝의 개요과 뉴럴 네트워크의 개요에 대해 살펴보고, 이런 딥러닝이 가진 문제점 중에 Underfitting에 대해 살펴보고 이에 대한 해결 방법에 관해 알아보았습니다. 다음 포스트에서는 이어서 딥러닝의 학습이 느린 이유와 이를 해결할 수 있는 방법에 대해 알아보도록 하겠습니다.

References



comments powered by Disqus
#deeplearning #machinelearning #dl #ml #sigmoid #relu #underfitting #overfitting #neuralnetworl #dnn