딥러닝(Deep Learning) 살펴보기 2탄

지난 포스트에 Deep learning 살펴보기 1탄을 통해 딥러닝의 개요와 뉴럴 네트워크, 그리고 Underfitting의 문제점과 해결방법에 관해 알아보았습니다. 그럼 오늘은 이어서 Deep learning에서 학습이 느린 문제점을 어떠한 방식으로 해결하고 연구하고 있는지 한번 알아보도록 하겠습니다.

Neural Network 복습

기존의 뉴럴 네트워크는 weight parameter들을 최적화(optimize)를 하기 위하여 Gradient Descent 방법을 사용했습니다. 그럼 Gradient Descent에 대하여 알아보도록 하겠습니다.

Gradient Descent

뉴럴 네트워크의 loss function의 현 weight의 기울기(gradient)를 구하고 loss를 줄이는 방향으로 업데이트(조정)해 나가는 방법을 통해서 뉴럴 네트워크를 학습하였습니다. loss(cost) function이라는게 나왔군요. 뉴럴 네트워크에서 loss function은 무엇일까요? 간단히 설명하면 지금 현재의 가중치에서 “틀린정도"를 알려주는 함수이죠.

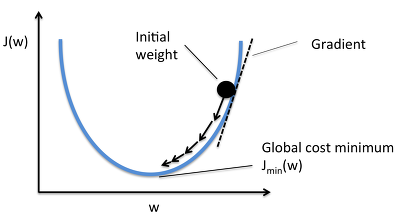
즉, 현재 네트워크의 weight에서 내가 가진 데이터를 다 넣어주면 전체 에러가 계산 되겠죠? 거기서 미분을 하면 에러를 줄이는 방향을 알 수 있습니다. 바로 위의 그림과 같이 말이죠. 그 방향으로 정해진 스텝량(learning rate)을 곱해서 weight을 이동시킵니다. 이걸 계속 반복해서 학습을 하는 것이죠. 수식을 간단히 살펴보면, 아래와 같습니다. 풀어서 보면 어려운 감이 있지만 하나하나 보면 그래도 조금은 이해할 수 있을거 같군요.

그러나 기존의 Gradient Descent 방식에는 크나큰 단점이 있었습니다. 위에서 적은 내용을 보시게 되면 한가지 큰 문제점을 발견할 수 있습니다.

내가 가진 데이터를 다 넣어주면 전체 에러가 계산 되겠죠?

바로 이 부분입니다. 최적값을 찾아 나가기 위해서 한칸 전진할 때마다 모든 데이터 셋을 넣어주어야 한다는 것이죠. 그래서 학습이 굉장히 오래 걸리는 문제가 발생하게 되는 것이죠. 언제 다 학습시킬 것인가라는 문제가 발생한 것이죠. 그러면 Gradient Descent 말고 더 빠른 Optimizer는 없는지 연구자들이 고민을 하게 되죠 그래서 나온 것이 Stochastic Gradient Descent 입니다.

Stochastic Gradient Descent

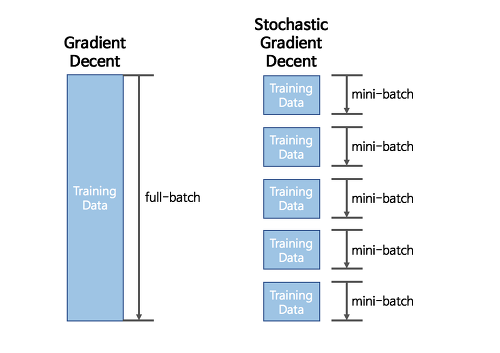
Stochastic Gradient Descent(이하 SGD)의 아이디어는 간단합니다. 바로 조금만 훑어보고(Mini batch) 빠르게 가봅시다라는 것이죠. GD와 SGD의 차이를 간단히 그림으로 비교해보면 아래의 그림과 같습니다.

최적값을 찾아가는 과정을 비교하는 그림을 살펴보면 조금더 쉽게 이해하실 수 있을 것입니다.

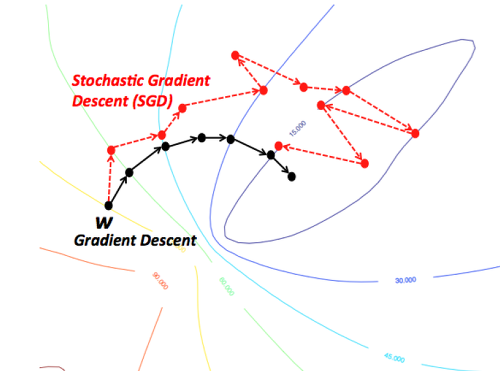
GD의 경우 항상 전체 데이터 셋을 가지고 한발자국 전진할 때마다(learning rate) 최적의 값을 찾아 나아가고 있는 모습을 볼수 있습니다. 그러나 SGD는 Mini-batch 사이즈 만큼 조금씩 돌려서 최적의 값으로 가고 있습니다. 그러나 최적값을 찾아 나아가는 과정을 봤을 때는 약간 뒤죽 박죽의 형태로 찾아가지만 속도는 GD 보다 훨씬 빠릅니다. 간단한 예제로 비교해보면 다음과 같습니다.

이렇게 해서 GD로 너무 오래 걸리는 학습 방법을 SGD를 통해 개선을 하였습니다. 그러나 SGD에도 문제점이 존재합니다. 미니 배치를 통해 학습을 시키는 경우 최적의 값을 찾아 가기 위한 방향 설정이 뒤죽 박죽입니다.

또 다른 문제점은 스텝의 사이즈입니다. 이것을 다른 말로 정의하면 learning rate입니다. 한걸음 나아가기 위한 보폭이 낮으면 학습하는데 오래 걸리고, 너무 크면 최적의 값을 찾지 못하는 문제가 있겠습니다.

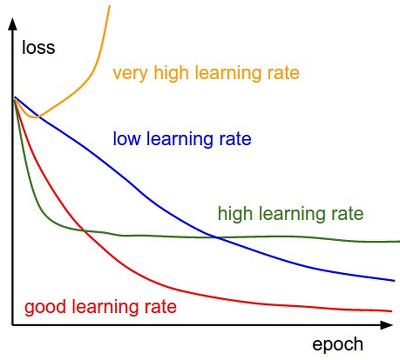
그래서 최근의 연구에서는 이러한 SGD의 문제점을 인지하고 각각의 문제점들을 개선하는 더 좋은 Optimizer들이 많이 있습니다. 새로운 Optimizer 들에 대해 알아보도록 하겠습니다.

Optimizer 계보

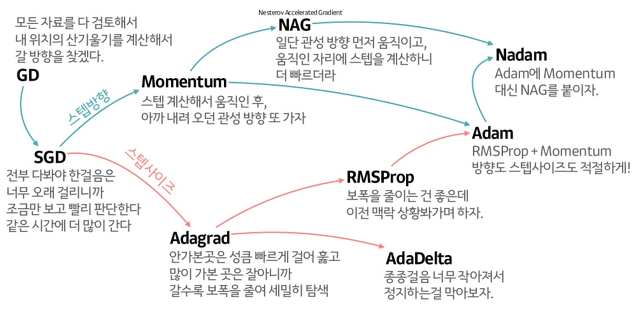
위의 자료는 references에 나와있는 하용호님의 슬라이드에 있는 내용입니다. Optimizer에 대해서 굉장히 손쉽고 이해하기 쉽게 정리를 해주셨습니다. 그림과 같이 SGD의 방향의 문제점을 집중적으로 개선한 알고리즘들부터 스텝 사이즈를 얼마나 하는게 좋을 것인가에 대한 알고리즘 2개로 나누어져 있으면 마지막엔 이러한 2가지 방법을 같이 사용한 알고리즘들이 나왔습니다. 그럼 한번 각 알고리즘의 성능에 관하여 그림으로 살펴보면 아래와 같습니다.

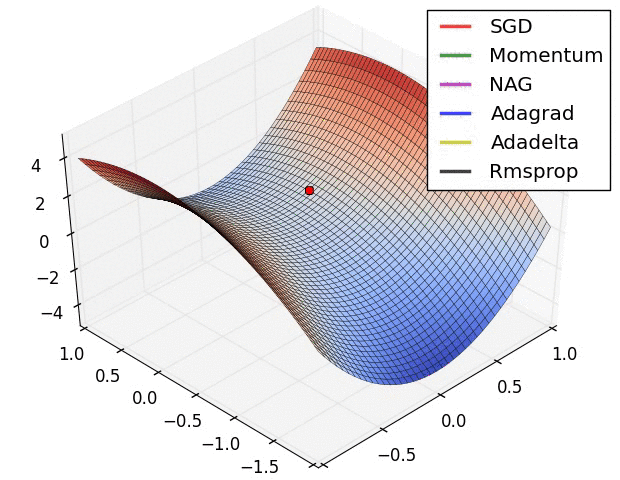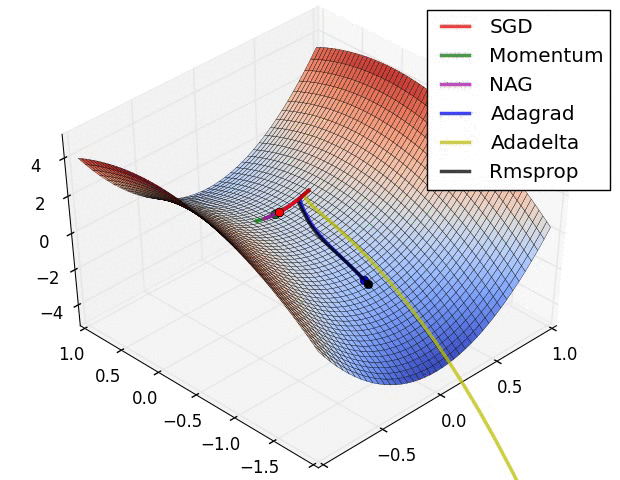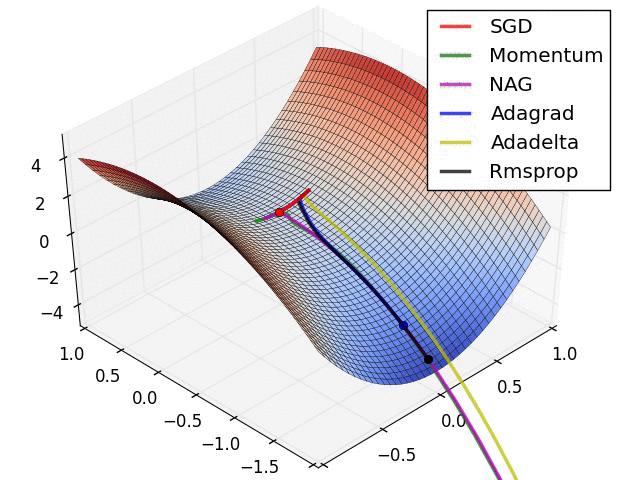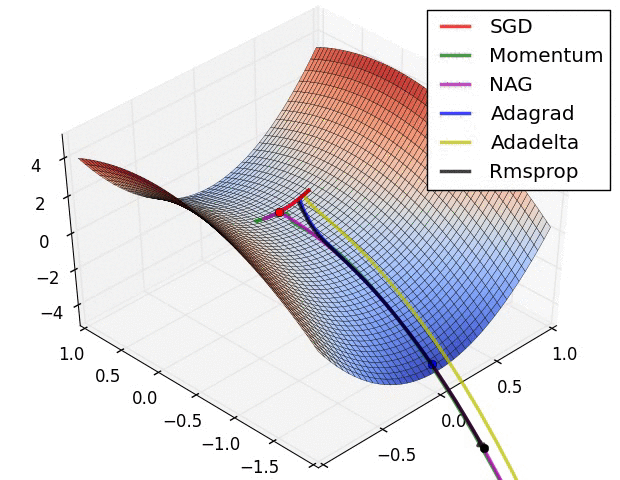
또 다른 그림으로 살펴볼까요?

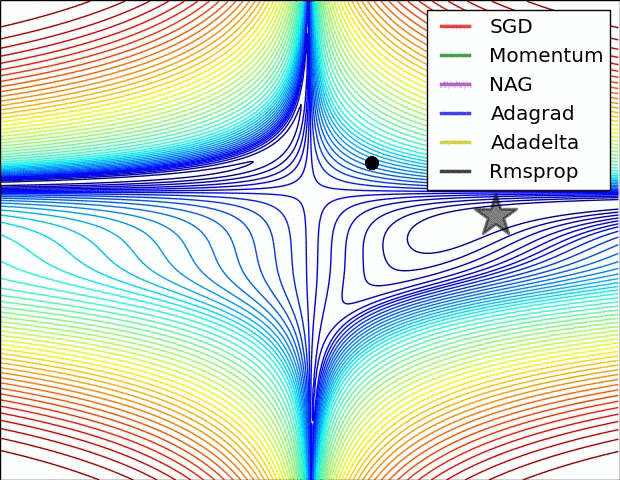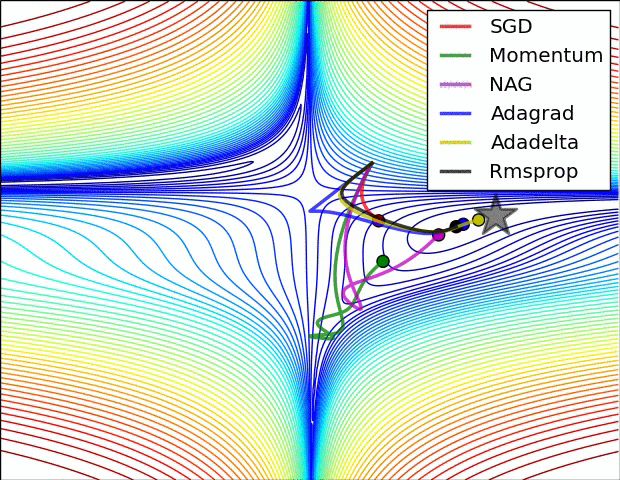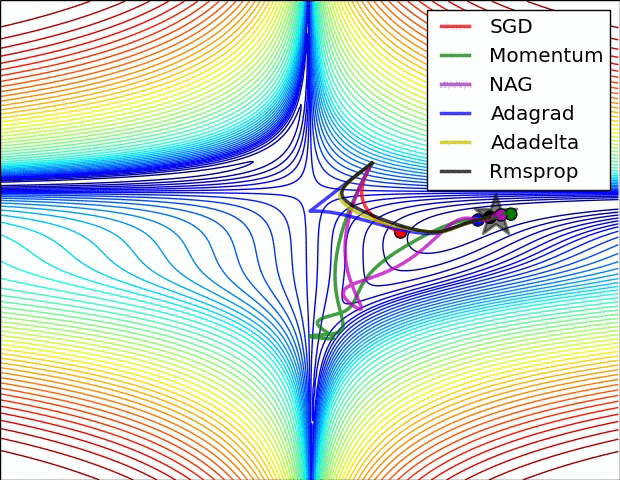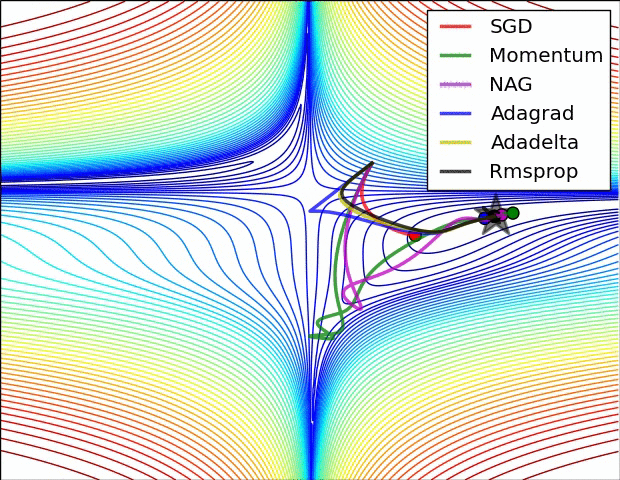
최근에 가장 많이 사용되는 Optimizer는 Adam을 많이 사용합니다. 대부분의 프레임워크에서도 지원을 하고 있고요. 이를 통해 기존의 SGD가 가지고 있는 문제점인 GD보다는 빠르지만 길을 헤메는 문제점을 개선시킨 버전들을 만들어서 더 빠르고 정확하게 최적을 값을 찾을 수 있는 알고리즘이 많이 나왔습니다.

결론

이번 포스트에서는 학습이 오래 걸리는 문제점의 원인에 대해 알아보았고 학습을 빠르게 하기 위해서 어떠한 방법으로 Optimizer가 개선되었는지에 대해 알아보았습니다. 오늘의 결론을 간략히 요약해 보면 다음과 같습니다.

Reference



comments powered by Disqus
#Deep Learning #딥러닝 #뉴럴네트워크 #gradient descent #GD #DNN #Stochastic Gradient descent #SGD #Adam #Optimizer #neural network